Ecuaciones paramétricas de la recta:
1. Dado el punto A(5,3) y el vector director (1, -2) , se pide:
a) Hallar las ecuaciones paramétricas de la recta r que determinan.
b) Obtener otros tres puntos cualesquiera de dicha recta.
c) Comprobar analíticamente si los puntos P(2,-1) y Q(3,7) pertenecen a r.
2. Dados los puntos A(1,3) y B(-1,6), se pide:
a) Hallar las ecuaciones paramétricas de la recta r que determinan.
b) Obtener otros tres puntos cualesquiera de dicha recta.
c) Comprobar analíticamente si los puntos P(7,-6) y Q(2,2) pertenecen a la recta.
Ecuaciones continua y general de la recta:
3. Con los datos del ejercicio 1, se pide:
a) Hallar las ecuaciones continua y general o implícita de la recta r que determinan.
(Soluc: 2x+y-13=0)
c) A partir de la ecuación general, obtener otros tres puntos cualesquiera de dicha recta.
d) Comprobar en ambas ecuaciones si los puntos P(2,1) y Q(3,7) pertenecen a r
4. Ídem con los datos del ejercicio 2 (Soluc: 3x+2y-9=0)
Todas las ecuaciones:
5. a) Hallar la ecuación de la recta que pasa por el punto A(3,5) y tiene la dirección del vector (2,-4)
en todas las formas posibles. (Soluc: 2x+y-11=0)
b) Ídem para el punto A(3,1) y el vector (4, -2) (Soluc: x+2y-5=0)
Miércoles 18 de Marzo
6. Determinar si el punto P(2,-1) pertenece a la recta 3x-2y+5=0. ¿Y el punto (1,4)? (Soluc: NO; SÍ)
7. Dada la recta ax+5y+4=0, determinar a para que la recta pase por el punto (2,-2) (Soluc: a=3)
8. a) Determinar, analíticamente, si los puntos A(3,1), B(5,2) y C(1,0) están alineados.
b) Ídem para A(1,1), B(3,4) y C(4,6)
c) Hallar k para que los puntos A(1,7), B(-3,4) y C(k,5) estén alineados. (Soluc: SÍ; NO; k=-5/3)
9. Calcular la ecuación de la recta que pasa por el punto A(-2,1/3) y tiene igual pendiente que la recta que pasa por P(2,1) y Q(3,4) (Soluc : y-1/3= 3 (x +2) )
Lunes 23 de Marzo
Martes 24 de Marzo
Viendo las dudas que me habéis preguntado sobre el ejercicio 11 de la clase de ayer, os voy a dejar un vídeo que quiero que veáis.
Actividades para hoy:
13. Calcula el área del triángulo que forman las siguientes rectas con los ejes:
a) y=3x+2
b) y= - 4x+1
c) y=2x+3
Solución actividad 13
Miércoles 25 de Marzo
Buenos días! Seguimos resolviendo dudas que me vais haciendo llegar. Algunos de vosotros tenéis dificultades para obtener las ecuaciones de los ejes coordenados (ejercicio 12). Os dejo un vídeo que espero os sirva de ayuda:
Y para hoy os voy a proponer el cálculo del área del triángulo que forman tres rectas. . Mirad primero el ejemplo del siguiente vídeo:
14. Para este triángulo calcula lo siguiente:
Solución actividad 14
Viernes 27 de Marzo
15. La recta que pasa por el punto M (2, 3) y es paralela a la recta r:y=3x+1 determina con los ejes coordenados un triángulo. Halla su área.
16. Calcular el ángulo que forman los siguientes pares de rectas:
El límite de una función nos proporciona información sobre su comportamiento. Por ejemplo, sobre su continuidad y las posibles asíntotas.
Es importante destacar el concepto de indeterminación o forma indeterminada:
Una indeterminación o forma indeterminada es una expresión algebraica que a veces aparece en el cálculo de límites y cuyo valor no se puede predecir, depende de la función del límite a calcular.
Por ejemplo, si una función tiende a 5/∞, entonces su límite es 0. Sin embargo, no sabemos de antemano el límite de una función que tiende a ∞/∞ (podría ser infinito o un valor finito). Por esta razón, decimos que ∞/∞ es una indeterminación.
Operaciones con infinitos:
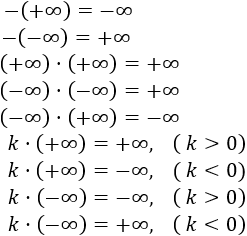
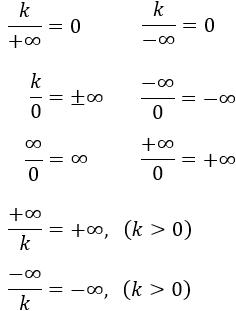
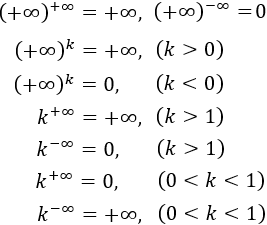
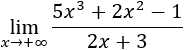
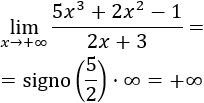
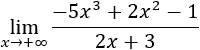
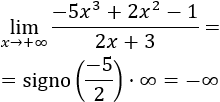
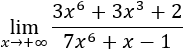
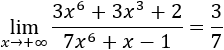
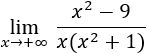
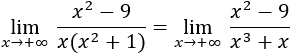
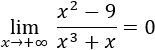
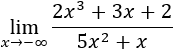
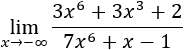
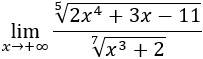
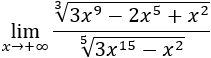
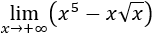
Soluciones límites
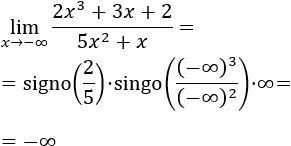
Recuerda que menos infinito al cubo es negativo porque está elevado a un exponente impar y menos infinito al cuadrado es positivo (exponente par).
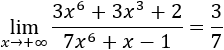
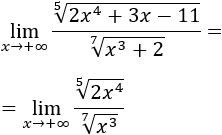
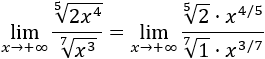
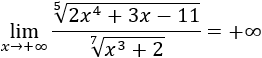
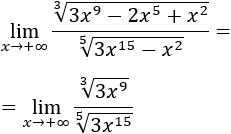
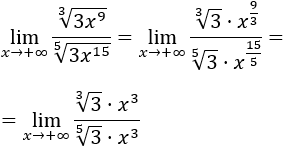
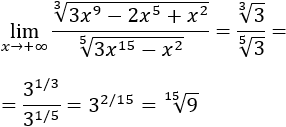
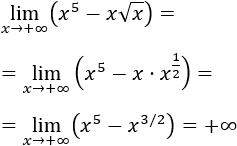
Lunes 23 de Marzo
10. Dada la recta que pasa por A(1,0) y B(3,4) se pide:
a) Hallar su forma paramétrica, continua y general.(Soluc: 2x-y-2=0)
b) ¿El punto (2,2) pertenece a dicha recta? (Soluc: si que pertenece)
11. Hallar el área limitada por la recta 5x+y-5=0, el eje de abscisas (y=0) y el eje de ordenadas (x=0). Hacer el dibujo. (Soluc: raíz de 5/2 u2)
12. a) ¿Qué ángulo forma la recta 3x-2y+6=0 con el eje de abscisas? (Soluc: 56º 18’ 36’’)
b) ¿Qué ángulo forma la recta 2x-y+5=0 con el eje de ordenadas? (Soluc: 26º 33’ 54’’)
Martes 24 de Marzo
Viendo las dudas que me habéis preguntado sobre el ejercicio 11 de la clase de ayer, os voy a dejar un vídeo que quiero que veáis.
Actividades para hoy:
13. Calcula el área del triángulo que forman las siguientes rectas con los ejes:
a) y=3x+2
b) y= - 4x+1
c) y=2x+3
Solución actividad 13
Miércoles 25 de Marzo
Buenos días! Seguimos resolviendo dudas que me vais haciendo llegar. Algunos de vosotros tenéis dificultades para obtener las ecuaciones de los ejes coordenados (ejercicio 12). Os dejo un vídeo que espero os sirva de ayuda:
Y para hoy os voy a proponer el cálculo del área del triángulo que forman tres rectas. . Mirad primero el ejemplo del siguiente vídeo:
Solución actividad 14
Viernes 27 de Marzo
15. La recta que pasa por el punto M (2, 3) y es paralela a la recta r:y=3x+1 determina con los ejes coordenados un triángulo. Halla su área.
16. Calcular el ángulo que forman los siguientes pares de rectas:
Solución actividad 15
Solución actividad 16
Lunes 30 de Marzo
LÍMITES
Una indeterminación o forma indeterminada es una expresión algebraica que a veces aparece en el cálculo de límites y cuyo valor no se puede predecir, depende de la función del límite a calcular.
Por ejemplo, si una función tiende a 5/∞, entonces su límite es 0. Sin embargo, no sabemos de antemano el límite de una función que tiende a ∞/∞ (podría ser infinito o un valor finito). Por esta razón, decimos que ∞/∞ es una indeterminación.
Operaciones con infinitos:
Sea un número real distinto de .
Sumas:
La resta es análoga. Por ejemplo,
Productos:
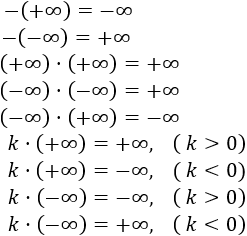
Observad que el producto de infinitos o el producto de infinito por una constante () es infinito.
El signo del resultado depende de la regla de los signos. Sin embargo, infinito por cero () es una indeterminación.
Cocientes:
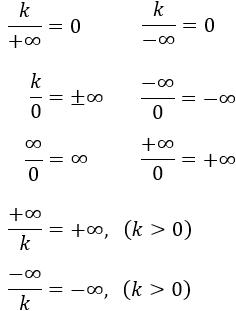
El cociente de ceros y el de infinitos es indeterminado.
Potencias:
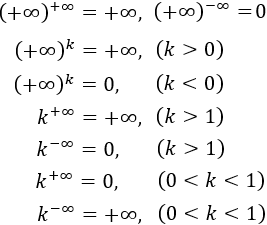
Las potencias , y son indeterminaciones.
Vamos allá con el cálculo de límites, empezamos con el cociente de dos polinomios, os acordáis, los que empezamos a ver en clase:
- Límite 1
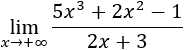
Tenemos la indeterminación infinito partido infinito.
Como el grado del polinomio del numerador es mayor que el del denominador, el límite es infinito:
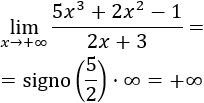
El infinito es positivo porque el cociente de los coeficientes principales de los polinomios es positivo.
- Límite 2
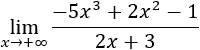
Razonamos como en el límite anterior:
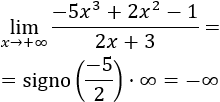
En este límite, el infinito del resultado es negativo porque el coeficiente principal del polinomio es negativo.
- Límite 3
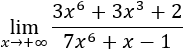
Como el grado del numerador es el mismo que el del denominador, el límite es el cociente de los coeficientes principales:
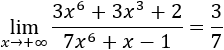
- Límite 4
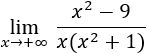
Tenemos un cociente de polinomios:
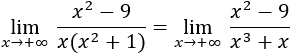
El grado del numerador es menor que el del denominador, así que
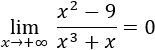
Actividad: Calcula los siguientes límites:
- Límite 5
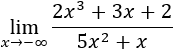
- Límite 6
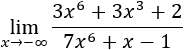
- Límite 7
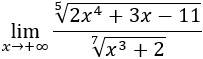
- Límite 8
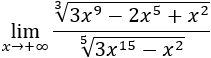
- Límite 9
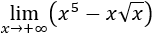
Soluciones límites
- Límite 5: Como el grado del numerador es mayor que el del denominador, el resultado es infinito, pero tenemos que calcular su signo:
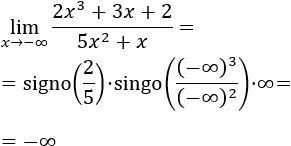
- Límite 6: Como el grado del numerador es el mismo que el del denominador, el límite es el cociente de los coeficientes principales:
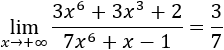
- Límite 7: Como los monomios que importan son los de grado mayor, podemos escribir:
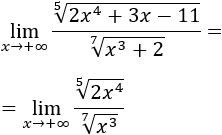
Escribiendo las raíces como potencias,
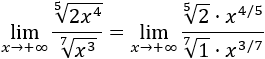
Como el grado del numerador es mayor que el del denominador, el límite es infinito:
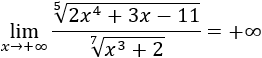
- Límite 8: Omitimos los monomios de grado menor porque apenas afectan al límite:
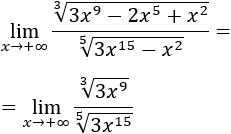
Operamos un poco para ver claramente los grados que tienen las :
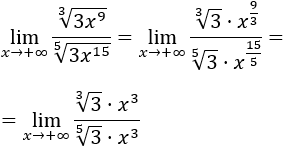
Como el grado del numerador es el mismo que el del denominador
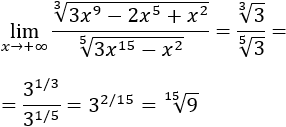
- Límite 9: Tenemos la indeterminación infinito menos infinito, pero fijaros bien, vamos a operar en el límite:
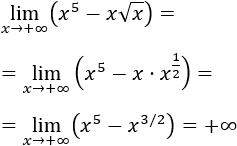
El límite es infinito porque tenemos infinito elevado a 5 menos infinito elevado a 3/2 (5 es mayor que 3/2). Es decir, prima el exponente mayor.
Martes 31 de Marzo
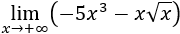
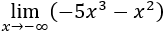
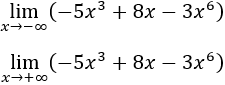
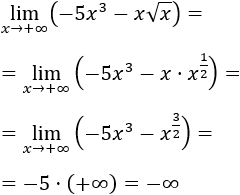
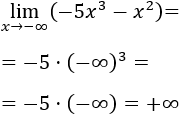
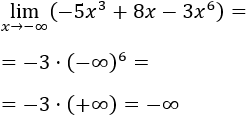
Martes 31 de Marzo
Actividad: Calcula los siguientes límites (fíjate en la solución del límite 9):
- Límite 10
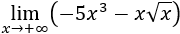
- Límite 11
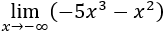
- Límite 12
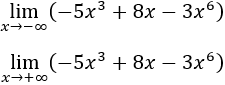
Soluciones
- Límite 10
Reescribimos el límite (escribimos la raíz como una potencia y operamos):
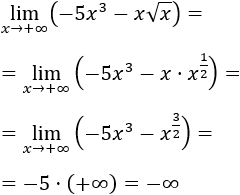
Observad que el signo negativo del coeficiente principal es la causa del signo negativo del infinito.
- Límite 11
Observad que tiende a infinito negativo.
Como prima el exponente mayor, tenemos:
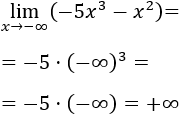
Observad que el cubo mantiene el signo negativo del infinito, pero el coeficiente negativo cambia el signo del infinito al multiplicarlo.
- Límite 12
Como prima el exponente mayor,
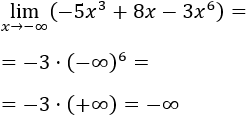
Observad que la potencia hace que el infinito sea positivo (porque 6 es par), pero el coeficiente cambia su signo.
Miércoles 1 de Abril
Ya hemos visto que cuando tenemos dos potencias de base x y queremos calcular el límite de la función cuando x tiende a infinito, la potencia de mayor exponente es un infinito de orden superior. Tenemos ejemplos en los límites 9, 10, 11 y 12. Pero ¿qué pasa cuando tenemos que comparar funciones que no sean potencias de base x? ¿Se pueden resolver esas indeterminaciones por comparación de infinitos? Veamos que nos dice la teoría:
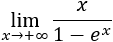
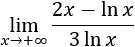
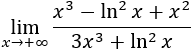
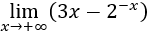
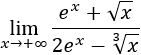
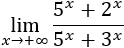
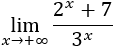
Solución límites miércoles
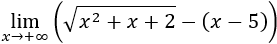
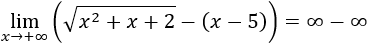
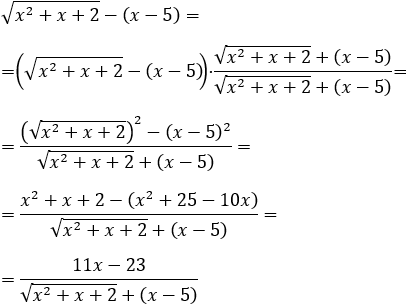
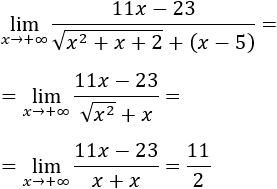
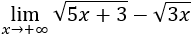
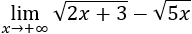
Martes 14 de Abril
Buenos días a tod@s!
Espero que estéis bien tanto vosot@s como vuestras familias. Nos espera un tercer trimestre inédito para todos, tanto para profesores como para alumnos, pero con vuestro trabajo vais a ser capaces de superar cualquier obstáculo que se ponga en el camino. Os felicito por el esfuerzo que habéis hecho durante estas primeras semanas y os animo a seguir en la misma línea para acabar el curso de la mejor manera posible.
Miércoles 15 de Abril
Hoy vamos a volver al inicio del tema, a aquellos límites que calculamos en la pizarra y entre tod@s. Es momento de ver si nos acordamos de cómo se hacen, y para ello, os propongo unos cuantos límites muy rápidos de calcular (nos olvidamos de las indeterminaciones por un día).
Actividades
Solución actividades
AVISO!!! Había una errata en la solución del límite 28 que ya está corregida.
Viernes 17 de Abril
Buenos días!
Vamos a acabar la semana con los límites con los que no fuimos de vacaciones de Semana Santa, con indeterminaciones infinito menos infinito en las que está implicada alguna raíz cuadrada.
Así, con estos límites, también repasamos las operaciones con raíces que vimos en la primera evaluación.
Miércoles 1 de Abril
Ya hemos visto que cuando tenemos dos potencias de base x y queremos calcular el límite de la función cuando x tiende a infinito, la potencia de mayor exponente es un infinito de orden superior. Tenemos ejemplos en los límites 9, 10, 11 y 12. Pero ¿qué pasa cuando tenemos que comparar funciones que no sean potencias de base x? ¿Se pueden resolver esas indeterminaciones por comparación de infinitos? Veamos que nos dice la teoría:
COMPARACIÓN DE FUNCIONES EN INFINITO
- Dadas dos funciones exponenciales (con x en el exponente) de bases mayores que uno, la de mayor base será un infinito de orden superior.
Ejemplo 1:
Dos elevado a infinito es superior a 1,5 elevado a infinito. Por tanto el límite de esta función es + infinito
Ejemplo 2:
Recordad que e es un número (e=2,71828182....) por tanto todas son funciones exponenciales. Comparamos las de mayor base; en el numerador es 4 elevada a x y en el denominador 4,01 elevado a x, por tanto como es mayor la del denominador el límite de esta función es cero.
- Cualquier función exponencial de base mayor que uno es un infinito de orden superior a cualquier potencia.
Ejemplo 1:
La función exponencial (denominador) es un infinito de orden superior a cualquier potencia (da igual el exponente). Por tanto el límite de esta función es cero (gana el denominador).
Ejemplo 2:
- Tanto las potencias de x como las funciones exponenciales son infinitos de orden superior a las funciones logarítmicas.
Actividad: Calcula los siguientes límites:
- Límite 13
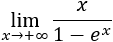
- Límite 14
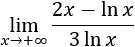
- Límite 15
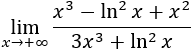
- Límite 16
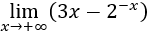
- Límite 17
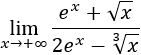
- Límite 18
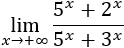
- Límite 19
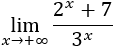
- Límite 13
Cualquier función exponencial de base mayor que uno es un infinito de orden superior a cualquier potencia.
- Límite 14
Tanto las potencias de x como las funciones exponenciales son infinitos de orden superior a las funciones logarítmicas.
- Límite 15
Tanto las potencias de x como las funciones exponenciales son infinitos de orden superior a las funciones logarítmicas.
Cualquier función exponencial de base mayor que uno es un infinito de orden superior a cualquier potencia. Como son del mismo orden las funciones exponenciales del numerador y denominador, el límite son los coeficientes que le acompañan.
- Límite 18
Dadas dos funciones exponenciales de bases mayores que uno, la de mayor base será un infinito de orden superior.
- Límite 19
Dadas dos funciones exponenciales de bases mayores que uno, la de mayor base será un infinito de orden superior.
Viernes 3 de Abril
¿Y si tenemos una indeterminación infinito menos infinito y comparando las funciones no podemos saber cual es el límite?
Fijémonos en el siguiente ejemplo:
Ejemplo.
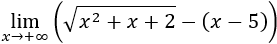
Tenemos una resta de infinitos:
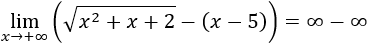
Multiplicamos y dividimos por el conjugado:
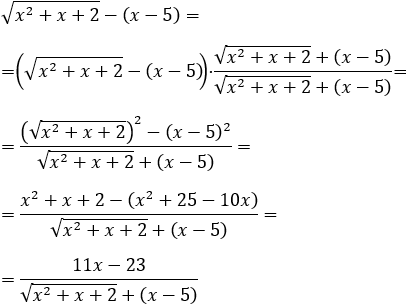
Así es más fácil calcular el límite:
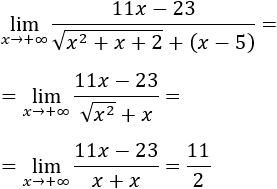
Actividad: Calcula los siguientes límites:
- Límite 20
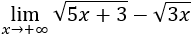
- Límite 21
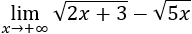
- Límite 22
Martes 14 de Abril
Buenos días a tod@s!
Espero que estéis bien tanto vosot@s como vuestras familias. Nos espera un tercer trimestre inédito para todos, tanto para profesores como para alumnos, pero con vuestro trabajo vais a ser capaces de superar cualquier obstáculo que se ponga en el camino. Os felicito por el esfuerzo que habéis hecho durante estas primeras semanas y os animo a seguir en la misma línea para acabar el curso de la mejor manera posible.
Vamos a seguir con la indeterminación infinito menos infinito pero ahora no
tendremos raíces implicadas, sino sumas de fracciones algebraicas. En este caso
debemos hacer el mínimo común múltiplo de los denominadores y sumar las dos
fracciones.
Miércoles 15 de Abril
Hoy vamos a volver al inicio del tema, a aquellos límites que calculamos en la pizarra y entre tod@s. Es momento de ver si nos acordamos de cómo se hacen, y para ello, os propongo unos cuantos límites muy rápidos de calcular (nos olvidamos de las indeterminaciones por un día).
Actividades
Solución actividades
AVISO!!! Había una errata en la solución del límite 28 que ya está corregida.
Viernes 17 de Abril
Buenos días!
Vamos a acabar la semana con los límites con los que no fuimos de vacaciones de Semana Santa, con indeterminaciones infinito menos infinito en las que está implicada alguna raíz cuadrada.
Así, con estos límites, también repasamos las operaciones con raíces que vimos en la primera evaluación.
Actividades
Solución actividades
Lunes 20 de Abril
Hola a tod@s!
Hemos trabajado ya algo con el infinito (cómo curiosidad os dejo el enlace a un artículo sobre el origen del símbolo matemático) pero hoy vamos a ver algo nuevo, que pasa cuando elevamos algo a infinito.
Actividades
Solución actividades
Martes 21 de Abril
Buenos días!
Hoy vamos a seguir practicando la indeterminación uno elevado a infinito y para ello os dejo dos límites mas.
A seguir practicando y para cualquier duda ya sabéis....estamos en contacto por el correo electrónico.
Actividades
Solución actividades
Lunes 27 de Abril
Hola, empezamos una semana más...
Hoy os voy a mostrar otra forma de resolver la indeterminación 1 elevado a infinito, se trata de una fórmula que deriva de la vista el lunes pasado. En los enlaces os dejo la teoría con dos ejemplos y ejercicios para que practiquéis.
Teoría fórmula para evitar indeterminación 1 elevado a infinito
Actividades
Solución actividades
Por supuesto, las dos formas vistas se pueden usar en todos los casos y el resultado del límite es el mismo. Para que podáis practicar más y ver que método os resulta más fácil os dejo los límites 49, 50, 51 y 52 resueltos de esta forma.
Límites 49, 50, 51 y 52 de otra forma
Miércoles 29 de Abril
Buenos días!
Como os anunciaba ayer nos queda una indeterminación, k/0. Hoy vamos a descubrir lo que son los límites laterales, cómo se calculan y que tienen que ver con esta indeterminación. Fijaros bien en los ejemplos que os explico a continuación.
Teoría indeterminación k/0
Actividades
Solución actividades
ENTREGA (Antes del Jueves a las 14:00)
Lunes 4 de Mayo
Buenos días!
Hoy vamos a empezar a derivar, y lo vamos a hacer usando la tabla de derivadas.
Lo primero que tenemos que saber es que si yo tengo una función f(x), su derivada se escribe como
f ´(x), por tanto, para indicar que estoy haciendo la derivada de una función le añado esa "prima".
Y ahora necesito saber cómo se deriva, y eso va a depender de la función que tenga para derivar, no será lo mismo una función potencial, que una función exponencial o una función logarítmica.
En la clase de hoy vamos a ver como derivar una potencia:
Recordad, "se baja el exponente y se le baja un grado al exponente", intentad hacer las siguientes actividades y me contáis cómo de difícil os resultó.
Actividades
Solución actividades
Actividades
Solución actividades
Solución actividades
Solución actividades
Martes 12 de Mayo
Hola a tod@s!
Lo primero que vamos a hacer hoy van a ser unos ejercicios en los que repasamos lo visto hasta ahora de derivadas (os dejo también las soluciones) para luego ver algo nuevo, la regla de la cadena.
¿Que será eso de la "regla de la cadena? os estaréis preguntando algunos....pues veamos un vídeo en el que nos lo explican:
Pues hoy vamos a utilizar la derivada del coseno
Actividades
Solución actividades
Solución actividades
Lunes 20 de Abril
Hola a tod@s!
Hemos trabajado ya algo con el infinito (cómo curiosidad os dejo el enlace a un artículo sobre el origen del símbolo matemático) pero hoy vamos a ver algo nuevo, que pasa cuando elevamos algo a infinito.
- ¿Qué pasa si elevamos infinito a infinito? Al multiplicar infinito por infinito infinitas veces pues nos da infinitamente infinito.
No es una indeterminación
- ¿Qué pasa si elevamos cero a infinito? Pues cero por cero infinitas veces es cero.
Cero elevado a infinito no es una indeterminación
- ¿Y si elevamos un número distinto de cero a infinito? Pues fíjate en el esquema:
Un número, distinto de cero y de uno, elevado a infinito tampoco es una indeterminación
- ¿Qué pasa con el uno? ¿Por qué no está incluido en el esquema anterior? Pues porque es una indeterminación.
Hoy vamos a ver cómo resolver la indeterminación uno elevado a infinito.
Actividades
Solución actividades
Martes 21 de Abril
Buenos días!
Hoy vamos a seguir practicando la indeterminación uno elevado a infinito y para ello os dejo dos límites mas.
A seguir practicando y para cualquier duda ya sabéis....estamos en contacto por el correo electrónico.
Actividades
Solución actividades
Lunes 27 de Abril
Hola, empezamos una semana más...
Hoy os voy a mostrar otra forma de resolver la indeterminación 1 elevado a infinito, se trata de una fórmula que deriva de la vista el lunes pasado. En los enlaces os dejo la teoría con dos ejemplos y ejercicios para que practiquéis.
Teoría fórmula para evitar indeterminación 1 elevado a infinito
Actividades
Solución actividades
Por supuesto, las dos formas vistas se pueden usar en todos los casos y el resultado del límite es el mismo. Para que podáis practicar más y ver que método os resulta más fácil os dejo los límites 49, 50, 51 y 52 resueltos de esta forma.
Límites 49, 50, 51 y 52 de otra forma
Martes
28 de Abril
Para calcular el límite
de una función cuando x tiende a un número se sustituye x por ese número y se
calcula. En caso de que el resultado final sea otro número ya hemos resuelto el
límite. Pero, como ya os imagináis tendremos indeterminaciones que tenemos que
aprender a resolver.
¿Qué dos
indeterminaciones nos podemos encontrar?
- 0/0
- k/0 donde k es un número real cualquiera
Fijaros que el
“problema” lo tenemos al dividir entre cero (indeterminación).
En la clase de hoy
vamos a ver cómo resolver indeterminaciones de la forma 0/0.
Miércoles 29 de Abril
Buenos días!
Como os anunciaba ayer nos queda una indeterminación, k/0. Hoy vamos a descubrir lo que son los límites laterales, cómo se calculan y que tienen que ver con esta indeterminación. Fijaros bien en los ejemplos que os explico a continuación.
Teoría indeterminación k/0
Actividades
Solución actividades
ENTREGA (Antes del Jueves a las 14:00)
Lunes 4 de Mayo
Buenos días!
Hoy vamos a empezar a derivar, y lo vamos a hacer usando la tabla de derivadas.
Lo primero que tenemos que saber es que si yo tengo una función f(x), su derivada se escribe como
f ´(x), por tanto, para indicar que estoy haciendo la derivada de una función le añado esa "prima".
Y ahora necesito saber cómo se deriva, y eso va a depender de la función que tenga para derivar, no será lo mismo una función potencial, que una función exponencial o una función logarítmica.
En la clase de hoy vamos a ver como derivar una potencia:
Recordad, "se baja el exponente y se le baja un grado al exponente", intentad hacer las siguientes actividades y me contáis cómo de difícil os resultó.
Actividades
Solución actividades
Martes 5 de Mayo
Buenos días!
Hoy vamos a derivar raíces, que no son más que potencias de
exponente fraccionario, por eso la fórmula que vamos a usar será la misma que
ayer. Mirad la explicación en el siguiente vídeo para luego hacer las
actividades que os propongo.
Actividades
Miércoles
6 de Mayo
Buenos días a tod@s!
No se os está dando mal
esto de derivar, hoy vamos a ver como se deriva una suma o resta de funciones
potenciales. Al igual que los días pasados os voy a dejar un vídeo para que
veáis y luego vayáis haciendo las actividades que os propongo.
Viernes 8 de Mayo
Buenos días!
En la anterior clase vimos como derivar sumas y restas de
funciones potenciales y hoy vamos a ver como derivar el producto.
Lunes 11 de Mayo
Hola a tod@s!
Si en la última clase estuvimos
practicando la derivada de un producto hoy vamos a ver como se deriva un
cociente. Visualiza el siguiente vídeo antes de intentar las derivadas que os
propongo.
Martes 12 de Mayo
Hola a tod@s!
Lo primero que vamos a hacer hoy van a ser unos ejercicios en los que repasamos lo visto hasta ahora de derivadas (os dejo también las soluciones) para luego ver algo nuevo, la regla de la cadena.
¿Que será eso de la "regla de la cadena? os estaréis preguntando algunos....pues veamos un vídeo en el que nos lo explican:
Miércoles 13 de Mayo
Buenos días!
De momento sólo hemos
estado trabajando con funciones polinómicas, hoy vamos a trabajar con una
función trigonométrica, el seno. Para ver como se deriva la función seno y cómo se aplica la regla de la cadena cuando hay una función seno implicada os dejo dos vídeos:
Viernes 15 de Mayo
Actividades
Solución actividades
Lunes
18 de Mayo
Buenos
días!
Hoy
vamos a ver como se derivan dos nuevas funciones:
Función
exponencial
Función
logarítmica (logaritmo neperiano)
Martes 19 de Mayo
Buenos días!
Vamos a empezar a repasar las características de las
funciones, y hoy trabajaremos el dominio. Para recordar cómo se calcula el
dominio de una función os dejo unos apuntes, un vídeo y unas actividades
interactivas:
Miércoles 20 de Mayo
Buenos días!
¿Os acordáis como se calculan los puntos de corte de una función con los ejes? Para recordarlo os dejo unos apuntes:
Solución actividades
Viernes 22 de Mayo
Buenos días!
Hoy vamos a ver que condición tiene que cumplir una función para ser simétrica, para ello os dejo unos apuntes para que miréis antes de hacer los ejercicios.
Apuntes de simetría
Actividades
Solución actividades
Viernes 22 de Mayo
Buenos días!
Hoy vamos a ver que condición tiene que cumplir una función para ser simétrica, para ello os dejo unos apuntes para que miréis antes de hacer los ejercicios.
Apuntes de simetría
Actividades
Solución actividades
Lunes 25 de Mayo
Hoy empezamos a trabajar las asíntotas de una función.
Existen tres tipos de asíntotas: horizontales, verticales y oblicuas.
Para saber cómo calcularlas fijaros en el siguiente vídeo:
Solución actividades
Martes 26 de Mayo
Buenos días! Vamos a seguir con las asíntotas.
Actividades
Solución actividades
Viernes 29 de Mayo
Lunes 1 de Junio
Hola a tod@s!
Hoy os voy a dejar la solución del dibujo de las asíntotas 2 y 3 y para mañana tenéis que hacer las tres que faltan.
Dibujo asíntota 2
Dibujo asíntota 3
Además, os voy a dejar unos ejercicios para los que tenéis suspensa la primera o segunda evaluación que debéis entregar antes de 12 de Junio.
RECUPERACIÓN 1ª EVALUACIÓN
RECUPERACIÓN 2ª EVALUACIÓN
Miércoles 3 de Junio
Buenos días! Hoy vamos a ver otro ejemplo de como se calcula el crecimiento o decrecimiento de una función, en este caso racional:
Viernes 5 de Mayo
Hola a tod@s, vamos a seguir viendo ejemplos de cálculo del crecimiento y decrecimiento de una función.
Lunes 8 de Junio
Hola! Hoy vamos a ver en que consiste el estudio completo de una función y lo vamos a hacer con un vídeo en el que explican la teoría de cálculo de dominio, simetría, puntos de corte, asíntotas, intervalos de crecimiento y decrecimiento, máximos y mínimos, curvatura de la función y puntos de inflexión. Éstos serán los pasos a realizar en este tipo de ejercicios, atentos al ejemplo:
Martes 9 de Junio
Hola! Hoy vamos a ver un ejemplo del estudio completo de una función racional:
Miércoles 10 de Junio
Veamos otro ejemplo del estudio completo de una función; a medida que vais viendo el vídeo debéis hacerlo en vuestro cuaderno:
Viernes 12 de Junio
En el estudio de las funciones podemos tener cualquier tipo de función, veamos hoy un ejemplo de función radical.
Lunes 15 de Junio
Buenos días de nuevo! Estamos acabando este curso tan atípico y lo vamos a hacer viendo más ejemplos de como se estudia una función. En este caso, y como último ejemplo, vamos a estudiar una función logarítmica:
Hoy vamos a ver como usar Geogebra online para graficar funciones. Éste tipo de aplicaciones pueden serviros para comprobar si habéis hecho bien un ejercicio en el que os pidan analizar y representar una función.
Viernes 19 de Junio
Hola a tod@s. Para finalizar este curso me gustaría compartir con vosotr@s un excelente trabajo que realizasteis hace un par de años como recuerdo de lo bien que lo pasábamos en clase. También os quisiera desear que paséis unas felices vacaciones y que el próximo curso la situación sanitaria nos permita volver a vernos como antes.
Martes 26 de Mayo
Buenos días! Vamos a seguir con las asíntotas.
Actividades
Solución actividades
Miércoles
27 de Mayo
Hola a tod@s!
Hoy vamos a dibujar las asíntotas horizontales y
verticales de los ejercicios del lunes y martes, para ello fijaros en el
siguiente ejemplo:
Buenos días a tod@s!
Dado que much@s de vosotr@s habéis temido muchas dificultades para dibujar las asíntotas os voy a dejar la solución de la primera con explicaciones y quiero que a partir de esa intentéis dibujar las funciones 2 y 3 (del lunes).
Lunes 1 de Junio
Hola a tod@s!
Hoy os voy a dejar la solución del dibujo de las asíntotas 2 y 3 y para mañana tenéis que hacer las tres que faltan.
Dibujo asíntota 2
Dibujo asíntota 3
Además, os voy a dejar unos ejercicios para los que tenéis suspensa la primera o segunda evaluación que debéis entregar antes de 12 de Junio.
RECUPERACIÓN 1ª EVALUACIÓN
RECUPERACIÓN 2ª EVALUACIÓN
Martes 2 de Junio
Hola!
Vamos a ver una de las aplicaciones de las derivadas, el
estudio de funciones; y en concreto vamos a ver cómo se calculan los intervalos
de crecimiento y decrecimiento y los extremos relativos.
Buenos días! Hoy vamos a ver otro ejemplo de como se calcula el crecimiento o decrecimiento de una función, en este caso racional:
Viernes 5 de Mayo
Hola a tod@s, vamos a seguir viendo ejemplos de cálculo del crecimiento y decrecimiento de una función.
Lunes 8 de Junio
Hola! Hoy vamos a ver en que consiste el estudio completo de una función y lo vamos a hacer con un vídeo en el que explican la teoría de cálculo de dominio, simetría, puntos de corte, asíntotas, intervalos de crecimiento y decrecimiento, máximos y mínimos, curvatura de la función y puntos de inflexión. Éstos serán los pasos a realizar en este tipo de ejercicios, atentos al ejemplo:
Martes 9 de Junio
Hola! Hoy vamos a ver un ejemplo del estudio completo de una función racional:
Miércoles 10 de Junio
Veamos otro ejemplo del estudio completo de una función; a medida que vais viendo el vídeo debéis hacerlo en vuestro cuaderno:
Viernes 12 de Junio
En el estudio de las funciones podemos tener cualquier tipo de función, veamos hoy un ejemplo de función radical.
Lunes 15 de Junio
Buenos días de nuevo! Estamos acabando este curso tan atípico y lo vamos a hacer viendo más ejemplos de como se estudia una función. En este caso, y como último ejemplo, vamos a estudiar una función logarítmica:
Martes 16 de Junio
Hola a tod@s. Para finalizar este curso me gustaría compartir con vosotr@s un excelente trabajo que realizasteis hace un par de años como recuerdo de lo bien que lo pasábamos en clase. También os quisiera desear que paséis unas felices vacaciones y que el próximo curso la situación sanitaria nos permita volver a vernos como antes.
Felices vacaciones y cuidaros mucho!






















Soy David de 1 Bach no se hacer los ejercicio 11 y 12 del lunes 23 de marzo
ResponderEliminarPasos a seguir para resolver el ejercicio 11:
Eliminar- Calculamos la intersección entre la recta y el eje de abscisas (resolvemos el sistema formado por las ecuaciones 5x+y-5=0 e y=0) y obtenemos un vértice del triángulo (vamos a llamarlo A)
- Calculamos el otro vértice que llamaremos B como la intersección de las rectas 5x+y-5=0 y x=0.
- El tercer vértice del triángulo será C=(0, 0), el origen de coordenadas.
- El triángulo obtenido es un triángulo rectángulo (dibújalo).
- La base y la altura del triángulo serán los módulos de los vectores que unen los punto A C y A B.
Para resolver el ejercicio 12 tienes que sacar un vector director de cada recta y calcular el ángulo que forman los dos vectores despejando de la fórmula del producto escalar.
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarNo entiendo el ejercicio 9 del 18/03, tengo que calcular primero la pendiente con ambos puntos, o cómo? Un saludo!
ResponderEliminarTienen que tener el mismo vector director (o proporcional)
ResponderEliminar